Projects

Black Hole Entanglement Entropy from Causal Graphs
Entanglement entropy on causal graphs is suspected to be related to entropy calculations on Wolfram Model branchial graphs, the latter being more computationally expensive. The project aims to compute the entropy of a Schwarzschild Black Hole leveraging established formalism of Causal Set Theory for calculating entanglement entropy on causal graphs, with the ultimate goal of testing whether the area scaling law holds for discrete spacetime models. Black Hole causal graphs were obtained by discretizing spacelike hypersurfaces and computing the causal relations among events in consecutive hypersurfaces.
Representation Theory of Non-Abelian Magnetic Charges
We discuss the representation theory of non-abelian charges in physics, particularly magnetic monopoles, defined analogously to the well known case of electromagnetism. We start by presenting examples of charges and their emergence from physical symmetries. Next, we present concepts of representation theory that allow to generalise the discussion to non-abelian symmetries. We proceed to discuss charge in gauge theories, the distinction between electric and magnetic charges, and their relation through the Dirac quantisation condition. Lastly, using the tools developed in the previous chapters, we discuss how quantisation conditions can be derived for non-abelian charges.
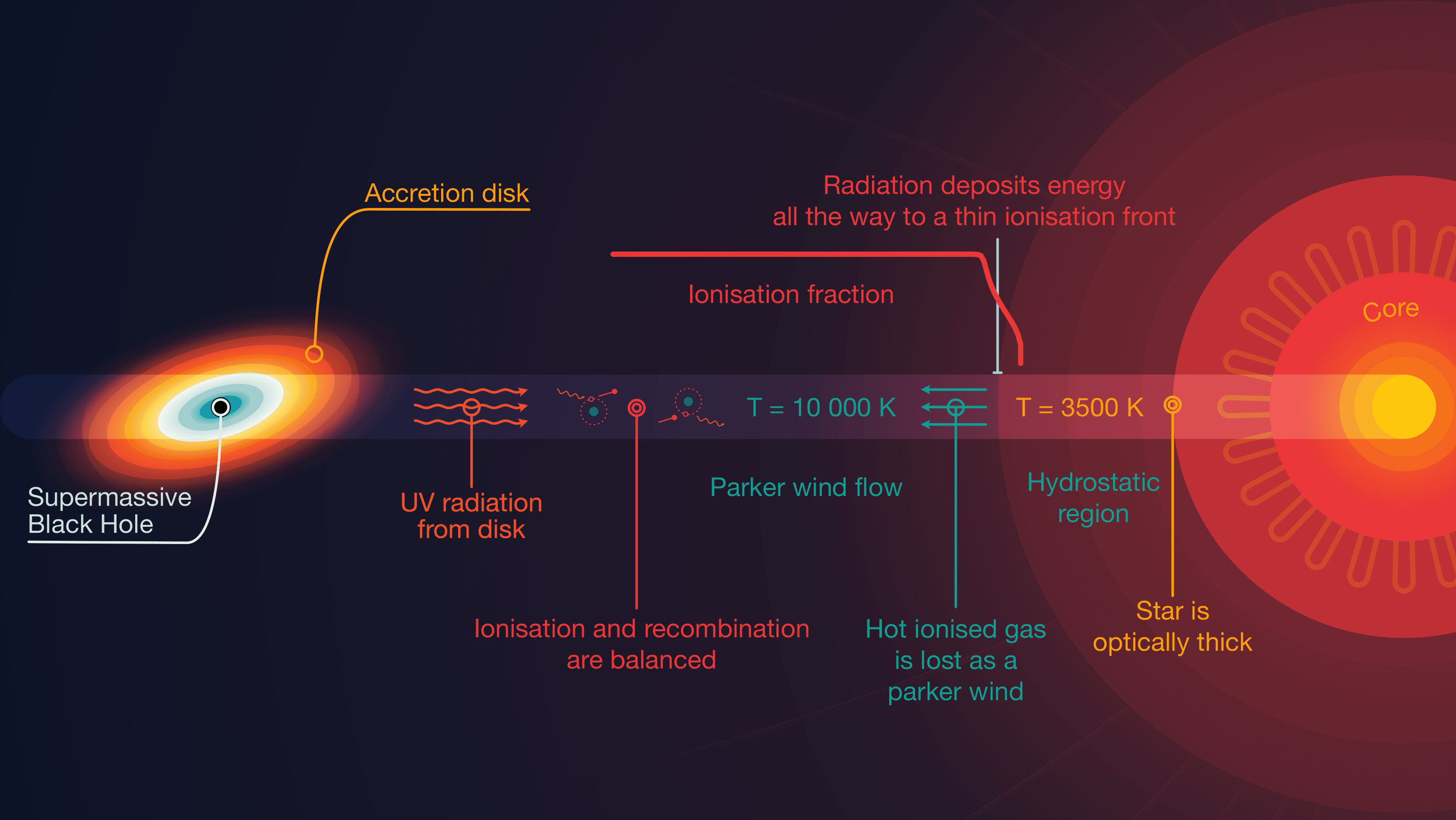
Shining Light on Missing Red Giants: Red Giant Photoevaporation in the Galactic Centre
The project’s aim was to investigate whether the lack of red giant stars at the center of the Galaxy could be explained by evaporation caused by radiation coming from the accretion disk of the central supermassive black hole. Our results provided promising evidence that photoevaporation can indeed significantly alter a red giant’s evolutionary course.